K. Qiu and A. Dogandžić
IEEE Trans. Signal Processing, vol. 58, pp. 2935-2952, Jun. 2010.
Abstract:
We propose a variance-component probabilistic model for sparse signal reconstruction and model selection. The
measurements follow an underdetermined linear model, where the unknown regression vector (signal) is sparse or
approximately sparse and noise covariance matrix is known up to a constant. The signal is composed of two disjoint
parts: a part with significant signal elements and the complementary part with insignificant signal elements that have
zero or small values. We assign distinct variance components to the candidates for the significant signal elements
and a single variance component to the rest of the signal; consequently, the dimension of our model’s parameter
space is proportional to the assumed sparsity level of the signal. We derive a generalized maximum likelihood
(GML) rule for selecting the most efficient parameter assignment and signal representation that strikes a balance
between the accuracy of data fit and compactness of the parameterization. We prove that, under mild conditions, the
GML-optimal index set of the distinct variance components coincides with the support set of the sparsest solution to
the underlying underdetermined linear system. Finally, we propose an expansion-compression variance-component
based method (ExCoV) that aims at maximizing the GML objective function and provides an approximate GML estimate of the significant signal element set and an empirical Bayesian signal estimate. The ExCoV method is
automatic and demands no prior knowledge about signal-sparsity or measurement-noise levels. We also develop
a computationally and memory efficient approximate ExCoV scheme suitable for large-scale problems, apply the
proposed methods to reconstruct one- and two-dimensional signals from compressive samples, and demonstrate
their reconstruction performance via numerical simulations. Compared with the competing approaches, our schemes
perform particularly well in challenging scenarios where the noise is large or the number of measurements is small.
Full paper download:
![]() (1.3 MB)
(1.3 MB)
(also available
in the IEEE Xplore Digital Library.)
Matlab code:
The Matlab code for the Expansion-compression Variance-component based method (ExCoV) proposed in the paper. All the
simulation results reported in the above paper can be reproduced from the package.
Please read the enclosed readme file as well. If you use this code in your research and publications, please refer to this paper.
![]() (Version 2.1, last updated Dec. 29, 2009)
(Version 2.1, last updated Dec. 29, 2009)
Features of
ExCoV:
ExCoV
is automatic and does not need any convergence tolerance level or threshold. Therefore, using
ExCoV
is easy: just input
- the measurement column vector and
- the sensing matrix (number of measurements by the
length of signal)
and
ExCoV
will do the rest. For more details on using
ExCoV
and running the demo, please refer to the readme file in the package.
Compared with competing approaches, ExCoV performs particularly well in challenging scenarios where the noise is large or the number of measurements is small, see the mean squared error curves below.
Illustrative Examples:
The following videos show the reconstruction
progress of our
ExCoV
algorithm. The sparse signal of length 512
contains 20 randomly placed binary spikes, taking values -1 or +1
with equal probability. We took 100 noisy measurements using a
Gaussian sensing matrix with orthonormalized rows and zero-mean
white Gaussian noise with variance 10-3. The
videos in the left and right panels correspond
to typical and atypical reconstructions, respectively, performed by
the
ExCoV
algorithm under the chosen simulation setup. The
atypical reconstruction corresponds to a difficult case. Following
the videos, we show Fig. 1 with the signal estimates of various
methods for the difficult case.
Figs. 2 and 3 show the average MSEs of various methods ) as functions of the number of measurements N, for binary sparse signals (Fig. 2) and Gaussian sparse signals (Fig. 3). The simulated sparse signals have length 512 containing 20 randomly placed non-zero elements. The sensing matrix is Gaussian with orthonormalized rows and the measurement noise is white Gaussian with mean zero and variance 10-5. To reproduce Figs. 2 and 3, please download version 2.0 of the code and run the simulation according to the readme file.
We demonstrate the reconstruction of the Shepp-Logan phantom of size 128 by 128 in Fig. 4 (a) from tomographic projections. The elements of the measurements are 2-D discrete Fourier transform (DFT) coefficients of the phantom image in Fig. 4 (a) sampled over a star-shaped domain, as illustrated in Fig.4 (b). We use Haar wavelet as the sparsifying basis and the effective sensing matrix for the sparse wavelet coefficients is a composition of selected rows of 2-D DFT matrix specified by the star shape in Fig.4 (b) and the inverse Haar wavelet matrix. Fig.4 (c)-(f) present the reconstructed images from the 30 radial lines given in Fig.4 (b) by filtered back-projection, normalized IHT, GPSR and approximate ExCoV, respectively. In Fig. 5, we vary the number of radial lines from 26 to 43, and, consequently, the measurement ratio N/m from 0.19 to 0.31. The codes for this tomographic imaging example have been included in the Version 2.1 package.
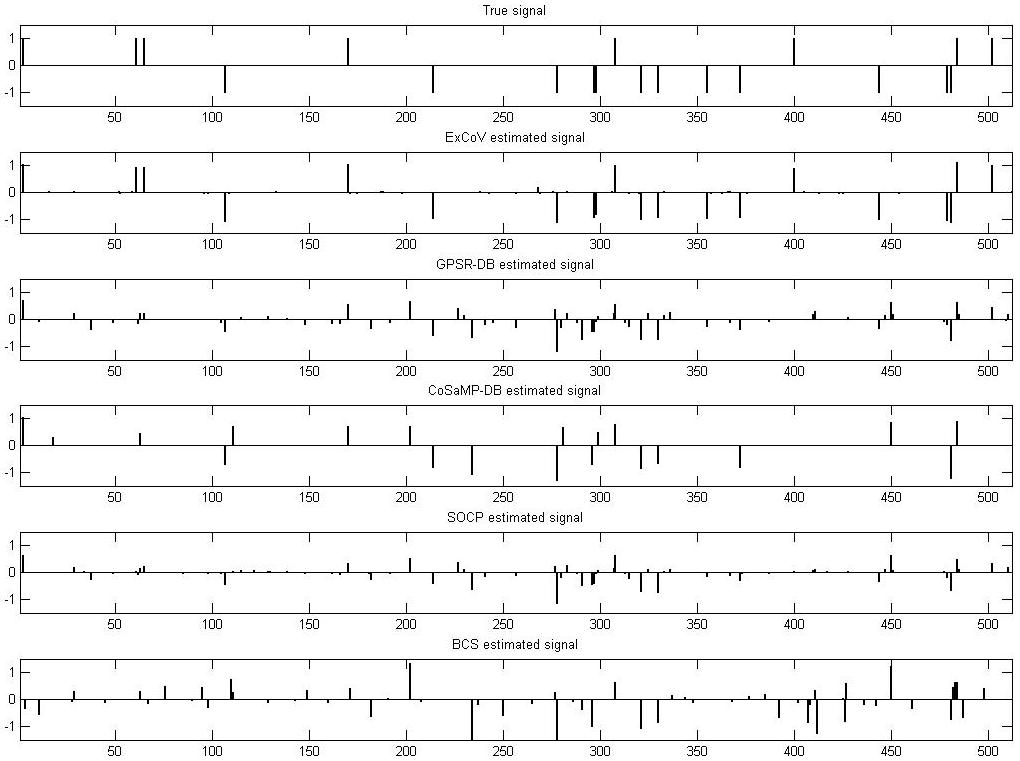
Fig. 1
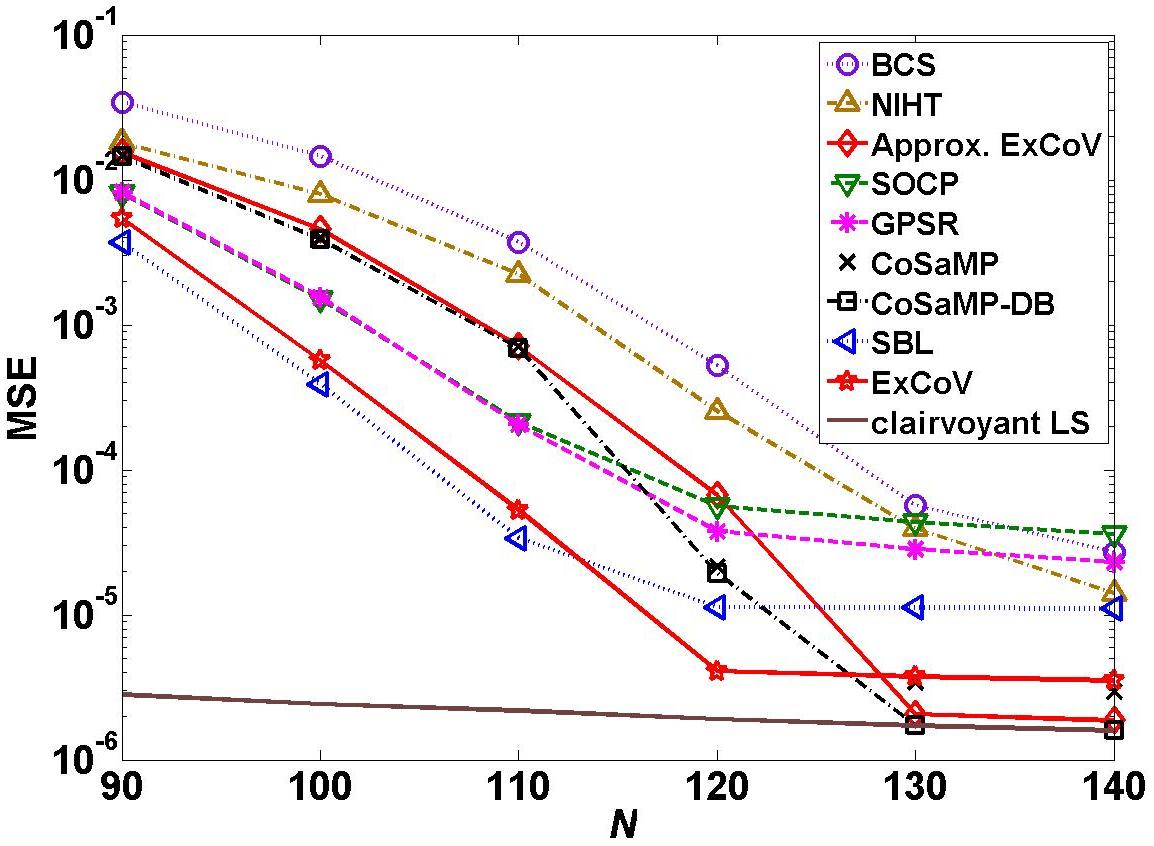
Fig. 2
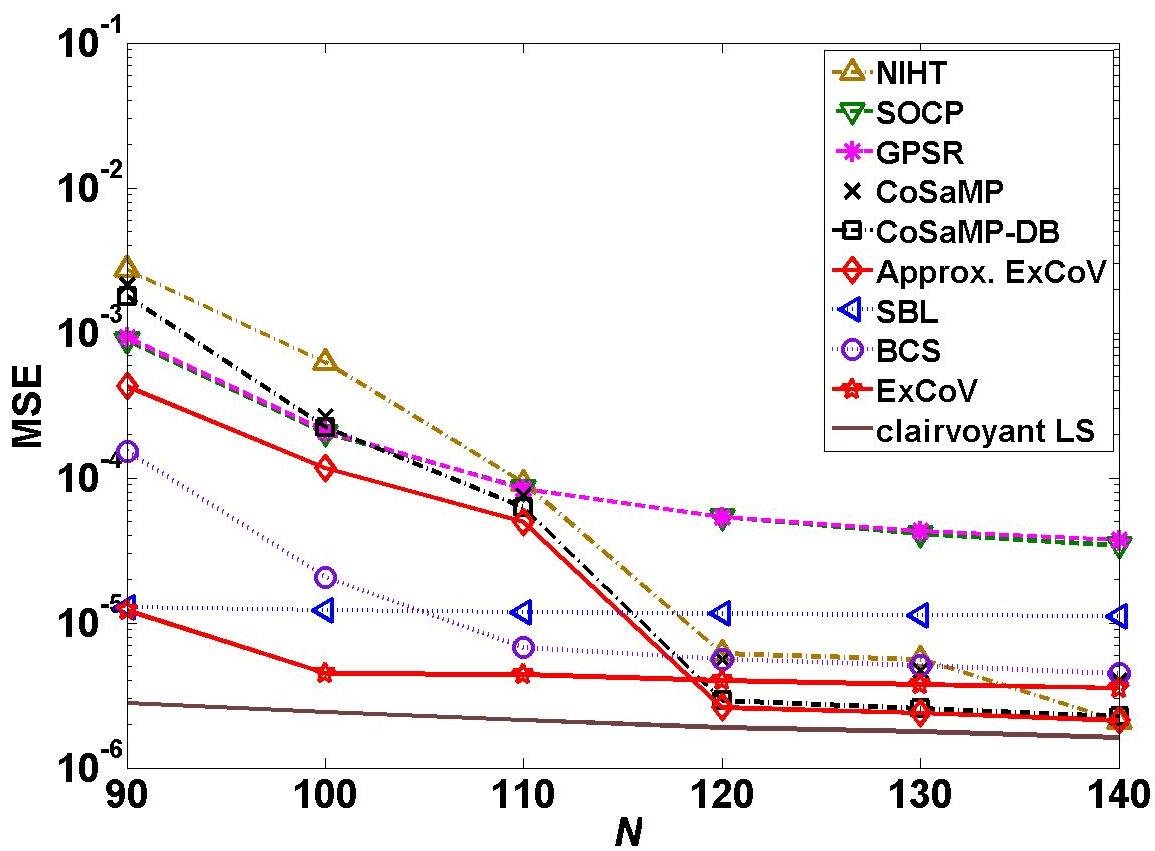
Fig. 3
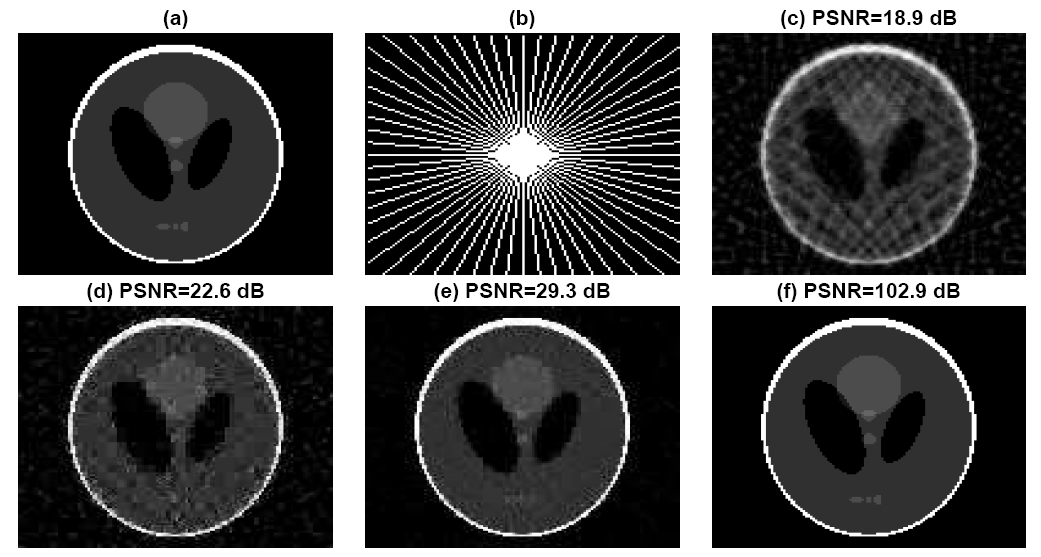
Fig. 4
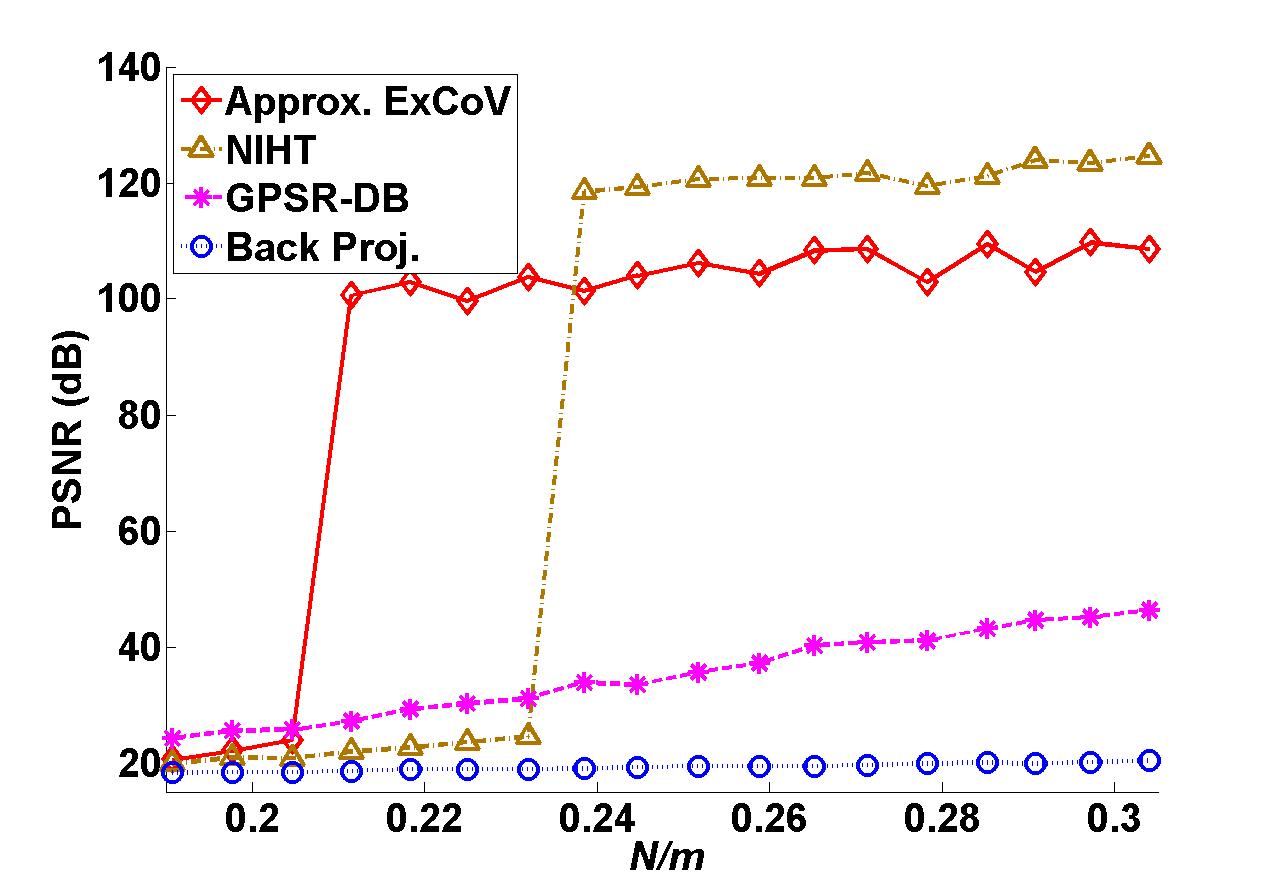
Fig. 5