Lipschitz's Adviser:      Johann Peter Gustav Lejeune Dirichlet 

Ph.D. Rheinische Friedrich-Wilhelms-Universität Bonn (Hon.) 1827
Dirichlet proved in 1826 that in any arithmetic progression with first term coprime to the difference there are infinitely many primes. Dirichlet is best known for his papers on conditions for the convergence of trigonometric series and the use of the series to represent arbitrary functions.

Poisson's and Fourier's Adviser:           Joseph-Louis Lagrange

 Lagrange excelled in many topics: astronomy, the stability of the solar system, mechanics, dynamics, fluid mechanics, probability, and the foundations of the calculus. He also worked on number theory proving in 1770 that every positive integer is the sum of four squares. In 1771 he proved Wilson's theorem (John Wilson) (first stated without proof by Waring) that n is prime if and only if (n-1)!+1 is divisible by n. In 1770 he also presented his important work Réflexions sur la résolution algébrique des équations which made a fundamental investigation of why equations of degrees up to 4 could be solved by radicals. The paper is the first to consider the roots of a equation as abstract quantities rather than having numerical values. He studied permutations of the roots and, although he does not compose permutations in the paper, it can be considered as a first step in the development of group theory continued by Ruffini, Galois and Cauchy.

Lagrange's Adviser:
Leonhard Euler
Ph.D. Universität Basel 1726
Euler was the most prolific writer of mathematics of all time.
He made decisive and formative contributions to geometry, calculus and number theory. He integrated Leibniz's differential calculus and Newton's method of fluxions into mathematical analysis. He introduced beta and gamma functions, and integrating factors for differential equations. He studied continuum mechanics, lunar theory with Clairaut, the three body problem, elasticity, acoustics, the wave theory of light, hydraulics, and music. He laid the foundation of analytical mechanics, especially in his Theory of the Motions of Rigid Bodies (1765).
We owe to Euler the notation f(x) for a function (1734), e for the base of natural logs (1727), i for the square root of -1 (1777), p for pi, 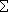for summation (1755), the notation for finite differences y and ²y and many others.
In 1737 he proved the connection of the zeta function with the series of prime numbers.
One could claim that mathematical analysis began with Euler. In 1748 in Introductio in analysin infinitorum Euler made ideas of Johann Bernoulli more precise in defining a function, and he stated that mathematical analysis was the study of functions. In Introductio in analysin infinitorum Euler dealt with logarithms. He published his full theory of logarithms of complex numbers in 1751.
The Mathematics Genealogy project lists Euler as Lagrange's adviser. Indeed, Euler did give substantial advice to Lagrange, although all of it was by mail. Lagrange studied Euler's work and corresponded extensively with him during the time when he wrote his early papers. Euler was also important in promoting Lagrange's career. This is why Euler is often viewed as his "adviser," even though Euler was in Berlin and Lagrange was in Torino.

Euler's Adviser:
Johann Bernoulli
1694
Bernoulli was  de l'Hôpital's tutor. However it did assure de l'Hôpital of a place in the history of mathematics since he published the first calculus book Analyse des infiniment petits pour l'intelligence des lignes courbes (1696) which was based on the lessons that Johann Bernoulli sent to him (without acknowledging that fact). The well-known de l'Hôpital's rule is contained in this calculus book and it is therefore a result of Johann Bernoulli. Bernoulli also made important contributions to mechanics with his work on kinetic energy.

Johann Bernoulli's Adviser:
Jacob Bernoulli
1676
Jacob Bernoulli's first important contributions were a pamphlet on the parallels of logic and algebra published in 1685, work on probability in 1685 and geometry in 1687. His geometry result gave a construction to divide any triangle into four equal parts with two perpendicular lines.
By 1689 he had published important work on infinite series and published his law of large numbers in probability theory. The interpretation of probability as relative-frequency says that if an experiment is repeated a large number of times then the relative frequency with which an event occurs equals the probability of the event. The law of large numbers is a mathematical interpretation of this result. Jacob Bernoulli published five treatises on infinite series between 1682 and 1704. The first two of these contained many results, such as fundamental result that 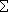(1/n) diverges, which Bernoulli believed were new but they had actually been proved by Mengoli 40 years earlier. Bernoulli could not find a closed form for 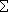(1/n²) but he did show that it converged to a finite limit less than 2. Euler was the first to find the sum of this series in 1737. Bernoulli also studied the exponential series which came out of examining compound interest.
In May 1690 in a paper published in Acta Eruditorum, Jacob Bernoulli showed that the problem of determining the isochrone is equivalent to solving a first-order nonlinear differential equation.

 
Jacob Bernoulli's Adviser:         Gottfried Wilhelm von Leibniz 

Leibniz's Adviser I:
Erhard Weigel
Ph.D. Universität Leipzig 1650

 
Leibniz's Adviser II:         Christiaan Huygens