\[ \newcommand{\cI}{\mathcal{I}} \newcommand{\dif}{\rm d} \]

Beam Hardening Correction via Mass Attenuation Discretization

Reference

Proc. IEEE Int. Conf. Acoust., Speech, Signal Process., Vancouver, Canada, May 2013, pp. 1085–1089. BibTeX

Abstract

We develop a beam-hardening correction method for polychromatic X-ray CT reconstruction based on mass attenuation coefficient discretization. We assume that the inspected object consists of an unknown single material and that the incident X-ray spectrum is unknown. In this case, the standard photon-energy discretization of the Beer’s law measurement equation leads to an excessive number of unknown parameters and scaling ambiguity. To obtain a parsimonious measurement model parametrization, we first rewrite the measurement equation in terms of integral expressions of the mass attenuation rather than photon energy. The resulting integrals can be discretized easily thanks to the fact that the range of mass attenuations is bounded and, in practice, fairly narrow. We then develop a constrained least-squares optimization approach for reconstructing the underlying object from log-scale measurements, where we impose the nonnegativity constraint to both the signal and the X-ray spectrum density estimates. We demonstrate the performance of the proposed method via a numerical example where we compare it with the standard FBP, which ignores the polychromatic nature of the measurements.

Index Terms

Beam hardening, computed tomography, signal reconstruction, X-ray tomography.

Background

According to the Lambert-Beer’s law, the fraction $\dif \cI / \cI$ of plane wave intensity lost in traversing an infinitesimal thickness $\dif\ell$ at Cartesian coordinates $(x,y)$ is proportional to $\dif\ell$, so that

\[ \frac{\dif \cI}{\cI} = - \mu(\varepsilon) \alpha(x,y) \dif\ell. \label{eq:beerLaw1} \]

where

$\mu(\varepsilon)$ is the mass attenuation coefficient of the material (in cm²/g), which depends only on the photon energy $\varepsilon$,
$\alpha(x,y)$ is the density map of the inspected object (in g/cm³).

Therefore, a monochromatic X-ray signal at photon energy $\varepsilon$ attenuates exponentially as it penetrates an object composed of a single material:

\[ \cI^{\text{out}} = \cI^{\text{in}} \exp\Bigl[ - \mu(\varepsilon) \int_\ell \alpha(x,y) \dif\ell\Bigr]. \label{eq:monotoneModel} \]

where $\cI^{\text{out}}$ and $\cI^{\text{in}}$ are the emergent and incident X-ray signal energies, respectively.

However, X-rays generated by vacuum tubes are not monochromatic. To describe the polychromatic X-ray source, assume that its incident following the density $\iota(\varepsilon)$, i.e.,

\[ \label{eq:constanttotalenergy} \int \iota(\varepsilon) \dif\varepsilon = \cI^{\text{in}}. \]

Then, the noiseless measurement collected by an energy integral detector upon traversing a straight line $\ell=\ell(x,y)$ is

\[ \cI^{\text{out}}=\int \iota(\varepsilon) \, \exp\Big[- \mu(\varepsilon) \, \int_\ell \alpha(x,y) \, \dif\ell\Big] \, \dif\varepsilon. \label{eq:polyModel0} \]

Main Idea

Assumption:

Both incident spectrum $\iota(\varepsilon)$ and mass attenuation function $\mu(\varepsilon)$ of the object are unknown.

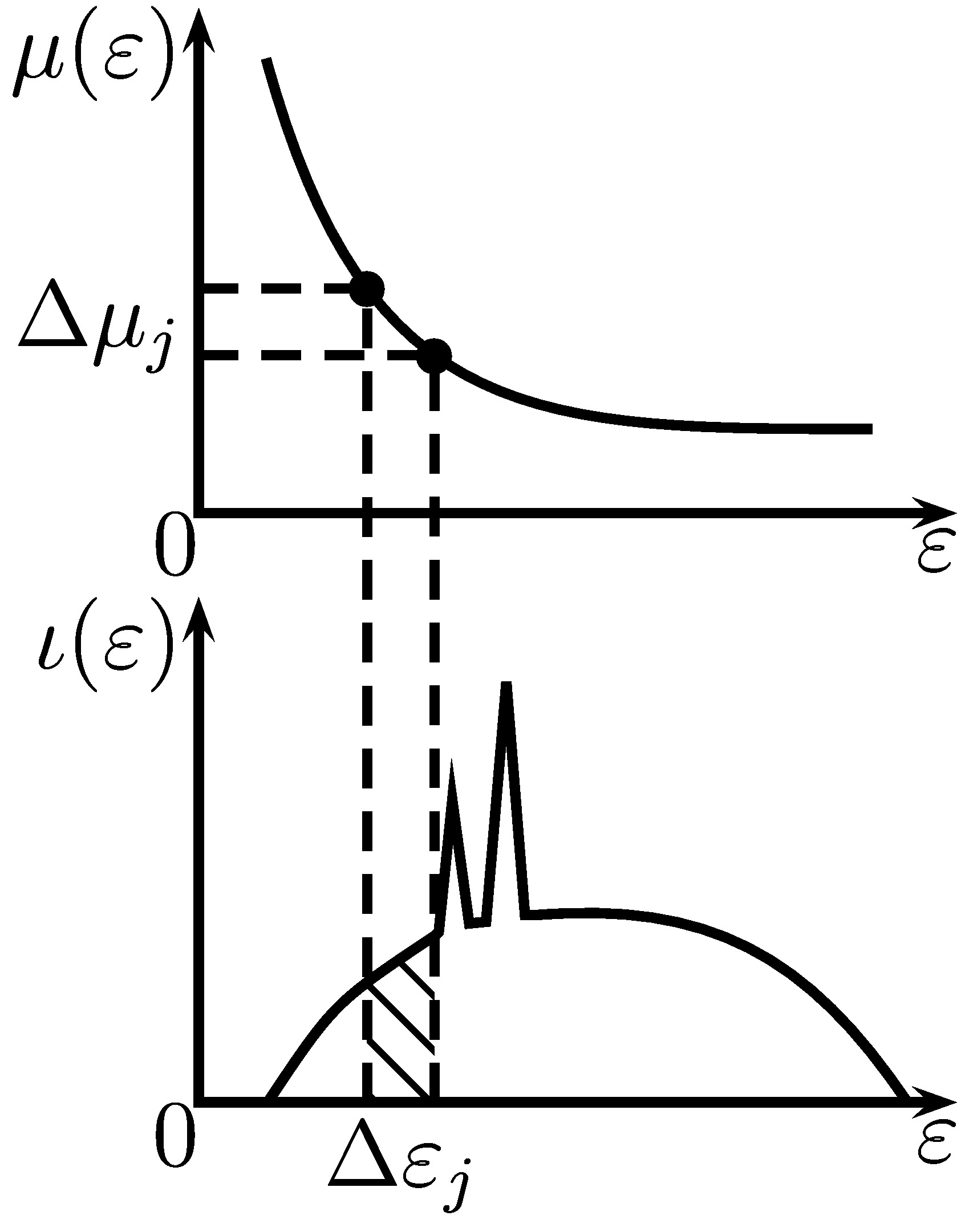
lebesgue

Objective:

Estimate the density map $\alpha(x,y)$.

Based on the fact that mass attenuation $\mu(\varepsilon)$ and incident spectrum density $\iota(\varepsilon)$ are both functions of $\varepsilon$, our idea is to:

write the model as integrals of $\mu$ rather than $\varepsilon$;
estimate $\iota(\varepsilon(\mu)) |\varepsilon'(\mu)|$ rather than $\iota(\varepsilon)$ and $\mu(\varepsilon)$.

For invertible $\mu(\varepsilon)$, define its inverse as $\varepsilon(\mu)$ and

\[ \mathcal{I}^{\mathrm{in}} = \int \iota(\varepsilon(\mu)) |\varepsilon'(\mu)| d\mu, \qquad \mathcal{I}^{\mathrm{out}} = \int \iota(\varepsilon(\mu)) |\varepsilon'(\mu)| \exp\Bigl[ -\mu \int_\ell \alpha(x,y) d\ell\Bigr] d\mu \]

Full paper download:

(1.2MB)

Poster for download:

(2.5MB)